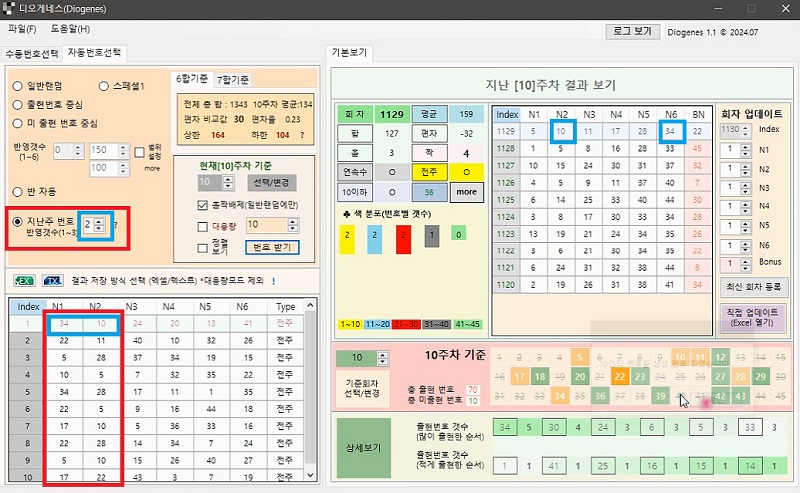
기존 1.1버전에 새기능이 추가된 1.1(up)버전을 업로드 합니다. (7/23일 기준)* 지난주 번호(즉, 최신 횟차의 번호중 몇개를 임의대로 집어넣고 조합합니다.) 다운은 여기서 디오게네스 업데이트 버전(버전명수정)Diogenes1.1(up)버전 : 지난주 결과값 반영하기 추가. (7/23일 기준)자세한것은 프로그램내 공지 참조.. -------------------------------------------------------------- ■ 업데이트 내역. (2024/7/23기준) ■ 1. 지난rosehill.tistory.com