바젤문제라고 하던가.. 오일러 관련 어떤 식을 보다가..
제곱은 정사각형이고.. 오브젝트들..
그 오브젝트들을 만들어 내고 있는 π제곱은 일종의 부모 클래스..(열린 정사각형.. )
(이 부모 클래스가 모든 사각형들에 미치고 있는 관계는, 결국 철학에서의 "부분과 전체, 전체이면서 부분, 부분이면서 전체"의 이야기... )
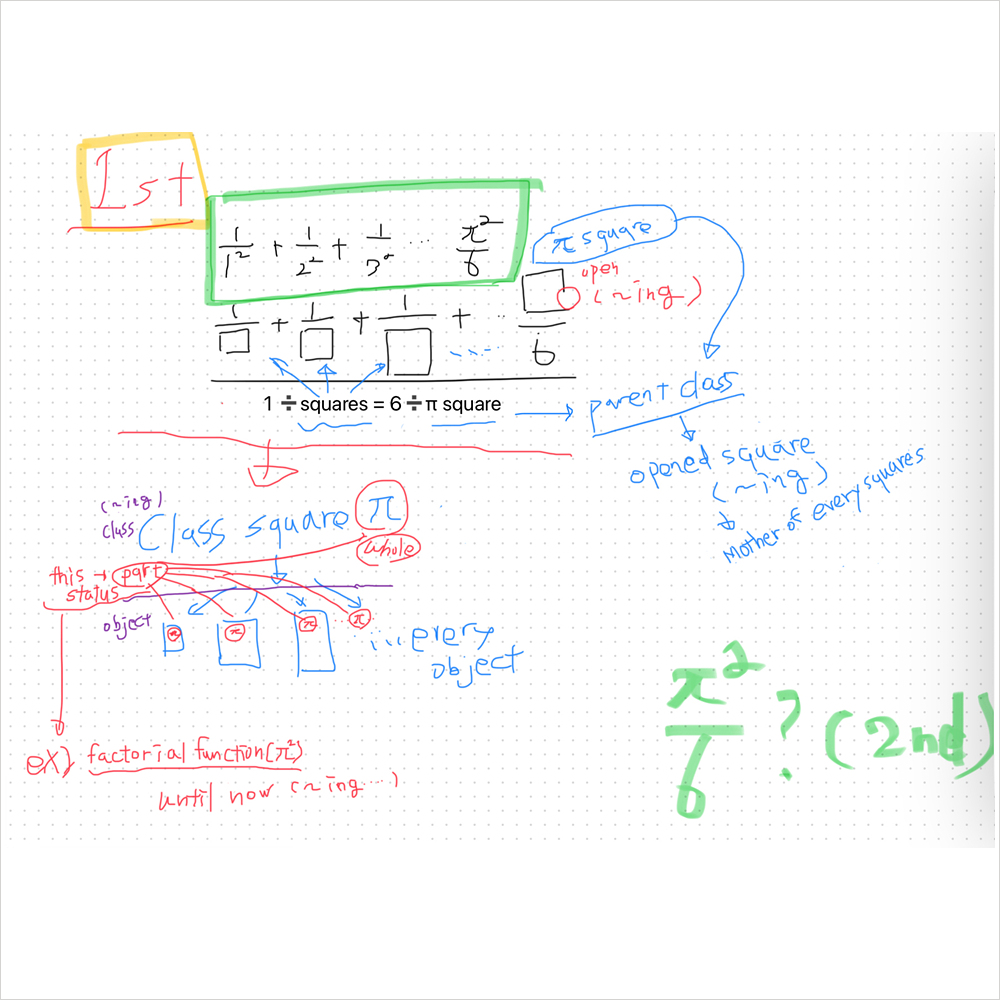
π제곱을 6으로 나눔은, 3으로 나눈것을 반으로 짜른것
여기서 부터 사각형의 외형이 아닌 내부적 운동 메커니즘이 들어감..
겉은 다 같은 정사각형이나 내부적으로 운동 궤적을 넣는다고 볼때, 차등이 생기는데..
3은 마방진의 세계에서 의미가 있는 숫자..3X3X3X3....마방진
(3의 거듭제곱 마방진만이 마방진의 기승전결 전체 궤도가 다 완성되는 일종의 ROYAL 마방진..)
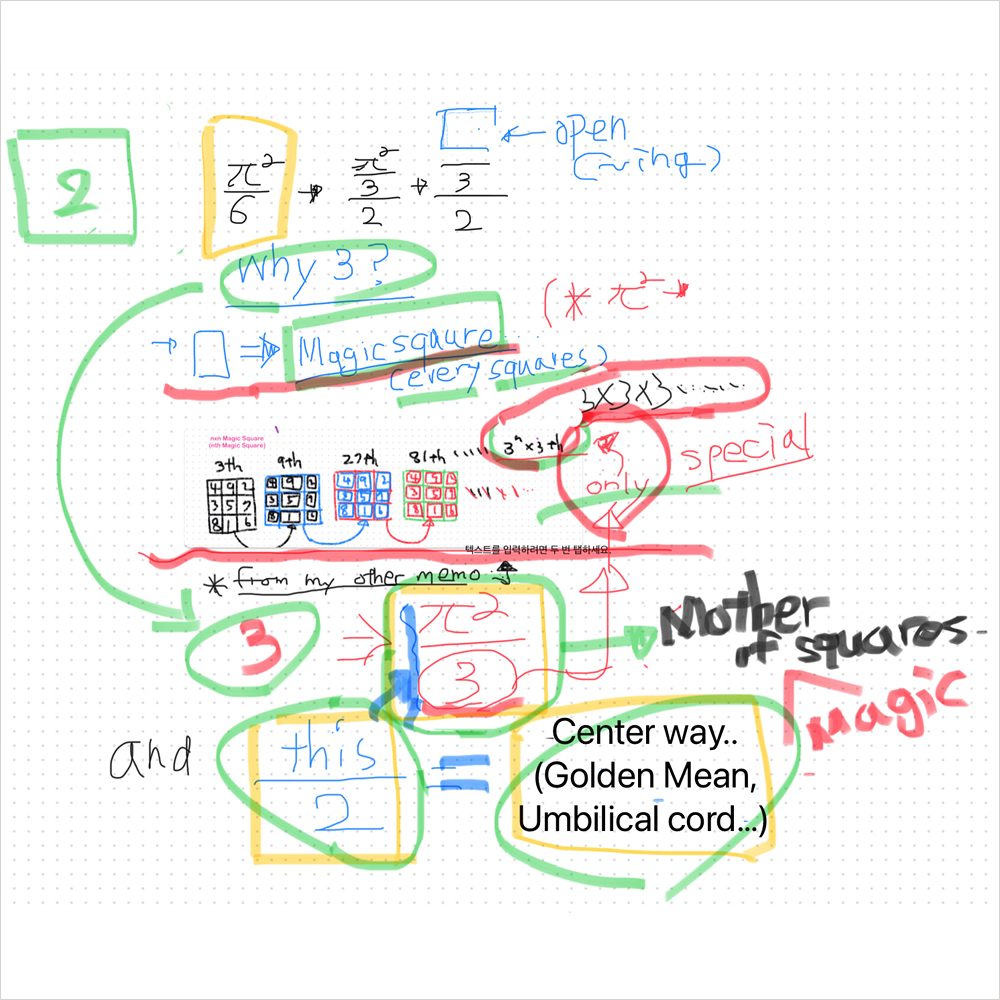
그것의 이등분은 결국 모든 정사각형의 세계에서 센터값,
그런데 현재까지 결과가 도출 되지 않는 π (파이)이므로..
계속 나아가는 하나의 길.. (way~)
(즉 중용값, 상위 클래스가 진행해 나가는 일종의 아리아드네의 끈 같은 길..)
* 부분과 전체.. : 철학에서 이야기 되는 부분들.. 나는 이것을 하나의 클래스와 서브 클래스의 관계로 해석할 수 있다고 봄..
예를들어 재귀함수를 통해, 팩토리얼을 구할때, 결과값을 만나지 않으면 이 재귀함수는 자기 자신을 무한히 호출 할 수 있슴..
(무수히 많은 부분이 됨.. 그런데 전체를 유지하고 있슴.. 리턴값에 도달하면 이제서 값을 도출하며 많은 오브젝트를 만들어 내고.. 자신은 다시 원래의 하나로 돌아옴.. 부분이면서 전체인 관계는 바로 이런 단계.. 리턴값을 만나지 못한 상태에서 모든 부분에 관여하고 있는 단계.. 실제 각 함수, 혹은 서브 클래스는 그것을 개인이 소유한것처럼 함수나 클래스내에 가지고 있지만 실제로는 그게아닌 그것이 이들에게 관여하고 있는것임.. 이때 이 재귀함수는 "부분이면서도 전체")
위를 예를 들자면, 재귀함수에 인자값을 π (파이) 제곱)을 넣으면 이 값이 끝나기 전까지는 전체이면서 무한의 부분인 상태가 됨.
만일 그때 급한대로 누군가 인위적으로 개입해 그냥 결과값을 도출한다면 나오긴 하겠으나 미완성인 상태로 나올것임..
현실적 존재들, 즉 오브젝트의 세계에서의 불완전함을 설명할 수 있는 이유.. 여기엔 어쩌면 수학도 포함됨..(괴델의 이야기)
느닷없이 떠오른 어떤 관념을.. 잊어버리기전에 끄적여 놓은 미완성 낙서 (끄적끄적, 뭐가됐던....) #1 (1차본..)
- 끝 -
* 6각형 형태의 마방진은 예외 .. (그러나,결국 4각형 마방진을 평행사변형으로 비튼 것..)456번이 대각선인데, 이것을 센터로 수직으로 놓은것에 불과하다고 봄..
* π (파이)는 원에 관여하고, π (파이)제곱은 사각형에 관여한다?
* π (파이)는 1차원에 관여하고, π (파이)제곱은 2차원에 관여한다.?
* π (파이)는 하나의 틈새이자 각도..? 마방진의 두께..? = 기본입자의 두께..?(나는 "하나의 입자"보다는 "어떤것의 최소단위"라고 보지만)
* 3차 마방진은 레이어 3개로 이뤄진 3층? 3번 4번사이에 ,6번7번 ,사이에
* 마방진은 편심된 형태..? (1,2,3과, 7,8,9의 편심.. 중심축이 4,5,6)
* 마방진 관련 생각은 몇년전에 낙서한것을 토대로.. 언제 길게 썰을 풀어볼까. 생각중..